Skip to content

Trajectory3D

class phaseportrait.Trajectory3D(dF, *, Range=None, dF_args={}, n_points=10000, runge_kutta_step=0.01, runge_kutta_freq=1, **kargs)

Inherits from parent class trajectory.

Gives the option to represent 3D trajectories given a dF function with 3 args.

Parameters

  • dF : callable

    A dF type function.

Key Arguments

  • Range : list

    Ranges of the axis in the main plot, by default None. See Defining Range.

  • dF_args : dict

    If necesary, must contain the kargs for the dF function, by default {}

  • n_points : int

    Maximum number of points to be calculated and represented, by default 10000

  • runge_kutta_step : float

    Step of 'time' in the Runge-Kutta method, by default 0.01

  • runge_kutta_freq : int

    Number of times dF is aplied between positions saved, by default 1

  • xlabel : str

    x label of the plot, by default 'X'

  • ylabel : str

    y label of the plot, by default 'Y'

  • zlabel : str

    z label of the plot, by default 'Z'

Methods

Inherits methods from parent class trajectory, a brief resume is offered, click on the method to see more information:

  • thermalize :

    Adds thermalization steps and random initial position.

  • initial_position :

    Adds a trajectory with the given initial position.

  • initial_positions :

    Adds multiple trajectories with the given initial positions.

  • plot :

    Prepares the plots and computes the values. Returns the axis and the figure.

  • add_slider :

    Adds a slider for the dF function.

Defining Range

  1. A single number. In this case the range is defined from zero to the given number in all axes.

  2. A range, such [lowerLimit , upperLimit]. All axes will take the same limits.

  3. Three ranges, such that [[xAxisLowerLimit , xAxisUpperLimit], [yAxisLowerLimit , yAxisUpperLimit], [zAxisLowerLimit , zAxisUpperLimit]]

Examples

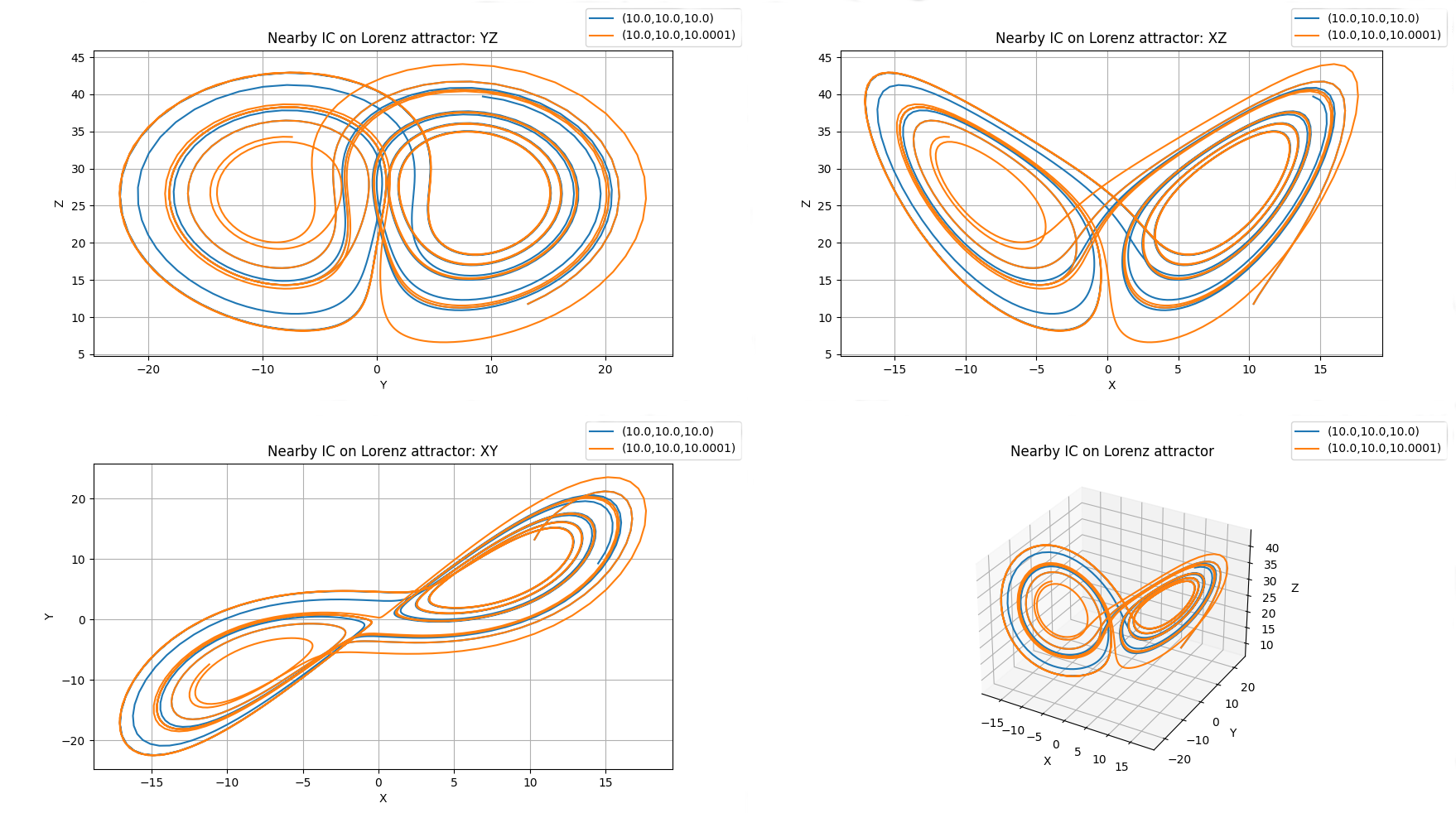
Lorentz attractor: chaos

Two trajectories with similar initial positions under the influence of Lorentz equations.

from phaseportrait import Trajectories3D

def Lorenz(x,y,z,*, s=10, r=28, b=8/3):
    return  -s*x+s*y, 
            -x*z+r*x-y, 
            x*y-b*z

a = Trajectory3D(
    Lorenz, 
    lines=True, 
    n_points=1300, 
    size=3, 
    mark_start_position=True, 
    Title='Nearby IC on Lorenz attractor'
    )

a.initial_position(10,10,10)
a.initial_position(10,10,10.0001)
a.plot()

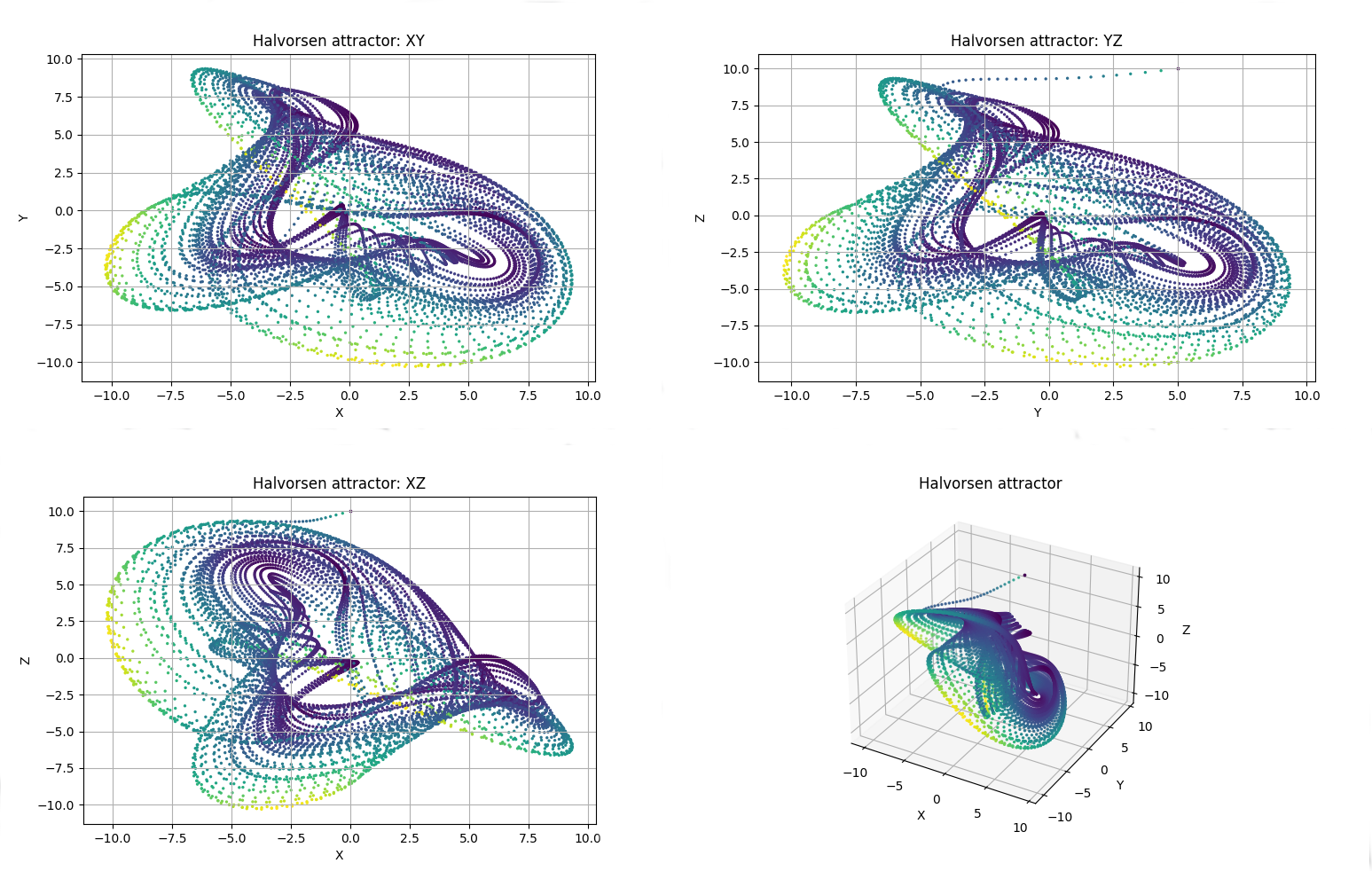
image

Halvorsen attractor

In this example we are interested in seeing the attractor, not trajectories, under the Halvorsen equations.

from phaseportrait import Trajectories3D

def Halvorsen(x,y,z, *, s=1.4):
    delta = (3*s+15)
    return  -s*x+2*y-4*z-y**2+delta, 
            -s*y+2*z-4*x-z**2+delta, 
            -s*z+2*x-4*y-x**2+delta

d = Trajectory3D(
    Halvorsen, 
    dF_args={'s':1.4}, 
    n_points=10000, 
    thermalization=0, 
    numba=True, 
    size=2, 
    mark_start_point=True, 
    Title='Halvorsen attractor'
    )

d.initial_position(0,5,10)
d.plot()

image